抽象的gydF4y2Ba
本文的基本目的是解决发展一个单一的,普遍的方程来描述在运动中的量子系统的所有波函数的问题。也就是说,能够解释它们所有可能的进化与它们可能遵循的可能路线有关。因此,我们将从分析量子波干涉的一个特殊情况开始,这是基于两个概率波的概念——由可能路径的叠加产生——这两个概率波由于马赫-曾德尔式干涉仪而相互作用。虽然这似乎是一种非常特殊的经历,但随着本文的深入,我们将看到如何将其推广以解释大量现象。因此,以下内容的重要性和超越依赖于这样一种想法,即当波函数干涉隐含时,它提供了一种评估量子演化的替代方法。总的来说,这是一项贡献,旨在丰富和完善我们对这一领域的理解,并促进与这些问题有关的繁琐计算过程。gydF4y2Ba
第一次实验的介绍gydF4y2Ba
想象一下下面的场景:一个普通的激光器,一个棱镜和一个投影屏幕被放置在桌子上并排成一行。激光的位置被安排得这样,当它发出的光到达棱镜时,它所描述的路径被分成两个相等的部分:其中一个穿过棱镜,另一个继续它在空气中的常规路径。我们在屏幕上看到的是干涉图案。我们知道,这是两个或多个波相互作用或干涉后形成的投影。一般来说,它看起来像是由几个较小的垂直条带组成的大的水平条带。gydF4y2Ba
干扰图案可以是许多不同布置的结果,但它们都可以减少到波浪相互作用的简单思想,并稍后崩溃,崩溃称为投影屏幕。在我们生活的相对大的世界中,只有大量减少的物理系统可以具有类似的波浪行为。例如,液体和一些水的流体具有可以容易地形成波的表面;然而,这些系统并不像自己的波浪一样:只有他们大多数外层都这样做。另一方面,古典光线确实在相当数量的情况下表现得像波浪。因此,直观地,我们之前提到的是,我们之前提到的是它具有产生干扰模式的能力。gydF4y2Ba
然而,在可能的最小尺度上,这种减少类波行为的想法就完全不同了。一旦我们到达量子力学的领域,我们看到的是粒子开始表现得像波一样。虽然这肯定是违反直觉的想法,但它却成为量子世界的本质。gydF4y2Ba
例如,在这篇论文中,我们将要做的事情在这一点上变得很明显:我们将把我提到的第一次经验转化为量子尺度,并使用量子物理定律来描述它。所有这一切背后的基本想法非常简单:我们最初拥有的激光——假设和在我们的心理实验中——将成为一个规模小得多的单个光子源。gydF4y2Ba
一旦我们成功地执行了这个转换并从前面提出的场景中推导出了法则,我们将推广这些条件和法则。在我们达到这个目标之后,很明显我们最初的假设可以用来描述大量的量子现象。gydF4y2Ba
普遍(实验量化)gydF4y2Ba
正如刚才提到的那样,我们的第一次假设是所提到的激光已成为单独的光源来源。原则上,此添加到尺度的变化 - 是量化我们的初始经验所需的一切。现在,源必须具有从中发出光子的区域。如果我们尝试描绘这个概念,我们可能会获得类似于这个的装置(图1)。gydF4y2Ba
显然,这意味着从该装置发出的任何光子都可以来自包含在圆形区域内的任何点。现在,让我们做出另一个假设:该区域被引导到棱镜,并且该装置以这样的方式放置,使得一半区域的一半通过棱镜和另一个通过外部平均值的方式被放置。如果我们在各个光子可以采取可能的路线的点放置探测器,我们将衡量发射的光子将通过平均值或棱镜的50-50个机会。到目前为止,我们的实验可以通过以下图像进行可视化(图2)。gydF4y2Ba
然而,假设没有一种方法来检测它们所走的路径,单个光子会发现自己处于两种可能状态的叠加,这两种状态与它们可能走的路径有关:通过棱镜或通过平均值。总的来说,我们将会有两波不同步的可能性,因为其中一波是不同的平均值意味着它的速度降低了。gydF4y2Ba
因此,我们会得到一个干涉模式。如果我们考虑到这一经验的经典版本,得到的模式将近似如下。gydF4y2Ba
注意关于图3的两件事是很重要的。首先,它是一个非常普遍的近似值,在经验中真正看到的。其次,很明显,量子世界和经典世界是不同的,尽管经验在原则上保持不变(我们的假设实验只是经典经验的量子类比)。因此,图3并不是在量子域中测量的一个完美的近似值。gydF4y2Ba
数学化实验的量子版本gydF4y2Ba
为了概括有关我们的经验的法律,它必须首先创建一套初始法律和方程。为此,我们将首先创建一个图表,并表示稍后将允许我们参加第一次将实验转换为数学语言的积分。图4显示了我们在这种情况下使用的表示法。gydF4y2Ba
从图形来看,我们可以描述由从源进入投影屏幕P中包含的未确定点的单个光子所拍摄的路线的总和gydF4y2BaxgydF4y2Ba.这个代数描述是由gydF4y2Ba
然而,这种形式的等式的问题:如果我们的目标是操作数字值,使我们能够计算分析的系统在x p的分析系统的概率,我们需要以复杂数字的语言编写的等式.如果我们假设以下(表1),则可以轻松解决此问题。gydF4y2Ba
表1:gydF4y2Ba求解复数语言。gydF4y2Ba
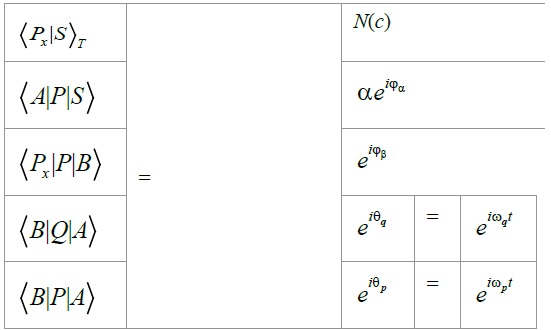
如果我们认为这是理所当然的,那么方程1就等于gydF4y2Ba
最后,如果我们对方程4进行归一化,就得到这个gydF4y2Ba
因为α只不过是复杂数字的常态,我们也可以写gydF4y2Ba
CgydF4y2Ba1gydF4y2Ba=αβ(8)gydF4y2Ba
和gydF4y2Ba是在投影屏幕中包含的点x中的光子着陆的概率。gydF4y2Ba
数学化前一个案例的变体gydF4y2Ba
如果我们打算概括我们的经验,我们要做的第一件事就是引入它的略有变化。由于相关问题,这种变化将是一个额外的棱镜。请记住,为了进行分析,我们将假设所涉及的棱镜并不相同。如果我们应用于1.1上使用的相同逻辑,我们的图表将如下所示(图5)。gydF4y2Ba
同样,我们要把这个新方程转换成数字符号。为了做到这一点,我们将把表2视为理所当然。gydF4y2Ba
表2:gydF4y2Ba数字符号。gydF4y2Ba

考虑到这一点,我们可以写新的等式gydF4y2Ba
对方程15进行归一化后,我们得到这个gydF4y2Ba
等式16和17处的值由表3定义。gydF4y2Ba
表3:gydF4y2Ba标准化方程式。gydF4y2Ba

这两种经验的空间概括gydF4y2Ba
在分析了前面的例子之后,很明显,方程中隐含的绝大多数术语取决于所使用的棱镜的数量。总的来说,我们看到的是,对于大量的棱镜,关于合成的归一化方程的形态发生下列关系:gydF4y2Ba
在这个等式中,n是复数的标准,而cgydF4y2BaygydF4y2Ba是一个实数和Z复数的乘积。重要的是考虑到这一点gydF4y2Ba
如果读者执行导致方程18的程序,就会变得很明显gydF4y2Ba
实验1:gydF4y2Ba
例如,在有五个棱镜的情况下,方程18的解是gydF4y2Ba
请注意,在没有任何棱镜的情况下也可以使用等式18,因为零棱镜的解决方案是gydF4y2Ba
总的来说,这在原则上与标准的标准化公式是一样的gydF4y2Ba
在哪里gydF4y2Ba是与状态φ相关的复数的标准。gydF4y2Ba
恢复丢失的信息gydF4y2Ba
如果仅使用先前暴露的泛化以简化X棱镜的情况,则有关在实验的余弦内隐含的角度的值的一些信息将会丢失。由于这个原因,现在我们将研究一种方法,允许我们恢复这些信息。gydF4y2Ba
第一步是绘制初始图形。然后,必须命名其中找到的相关点,就像在1.1和1.2中所做的那样。请注意,尽可能勤勉地复制第1节(1.1 & 1.2)中发现的案例是必要的。gydF4y2Ba
一旦定义了代数值,下一步就是添加每个单独的复数号内包含的所有角度,如下例所示:gydF4y2Ba
这将为我们提供一组角度,每个人都表示为gydF4y2Ba,其中x等于基团的数目。注意,组的总数(gydF4y2Ba)定义为gydF4y2Ba
如果gydF4y2Ba被定义为添加问题中涉及的每个复数的角度(在1.1的情况下,它将等于gydF4y2Ba;另一方面,1.2是(gydF4y2Ba),剩余角度的数量 -gydF4y2Ba- 应该相当于gydF4y2Ba
一个年代年代uming that we take these premises for granted, the recovery method becomes extremely simple: The first cosine’s angle will be the difference between the first group and the second one, the second angle related to a cosine will be the difference between the first group and the third one, etc. Once it is impossible to proceed by taking the first group as the first term in the subtraction, the second one will take its place.
请注意,一旦我们达到减法中的第一项是第二组的点,减法被定义为第二组和以下内部之间的差异。我们不考虑以前的任何一组。该逻辑也适用于关于哪个组占据减法中第一个术语位置的下一个班次。gydF4y2Ba
例如,在有两种棱镜的情况下,我们的方法(一旦完成)就是这样的(表4)。gydF4y2Ba
表4:gydF4y2Ba两种棱镜的方法。gydF4y2Ba

让我们根据我们的决议而考虑到这一点(表5)。gydF4y2Ba
表5:gydF4y2Ba最终决议。gydF4y2Ba

总体概括gydF4y2Ba
如果我们在2.1期间查看分析,则可以明显变得明显,等式18是普遍的,因为它可以应用于任何数量的棱镜,并且当没有任何棱镜时甚至是真的。现在,重要的是要记住我们从未真实地定义了我们以确切值放置的变量的事实。这种有关采取任何可能的容量的自由意味着我们的方程不仅适用于棱镜:无论用于产生干扰的平均值如何,它们都适用。它只是调整对等式的每个变量的精确值的问题。gydF4y2Ba
正如我们之前提到的,我们定义的方程在没有棱柱的情况下也是有效的。因此,可以接受的说法是,它们必须适用于任何旨在描述任何量子系统所采取的路线或可能路线的情况。这更适合描述一个系统的概率gydF4y2Ba位于XgydF4y2Ba一个gydF4y2Ba落在待定点X上gydF4y2BabgydF4y2Ba.如果我们考虑到这种表示法,可以更准确地重写等式18如下:gydF4y2Ba
为了最终确定这一概括,让我们考虑总体而言,可以通过波函数来描述每个单个量子状态,而不仅仅是链接到位移的概念。这意味着,鉴于在一种方法的角度下,描述与位置相关的状态之间没有原理差异,并且任何其他一个(例如,与电子的旋转连接),等式31也可用于描述进化我们想要评估的任何其他国家。实际上,我们使用棱镜的事实意味着我们还考虑了一般的演变,因为这些意味着系统的波长阶段的变化。我t一个llcomes down to matter of changing the interpretation of our evaluation, in terms of the exposure to a certain evolution, from distance to time (e.g, the prisms exposed a system to an evolution for a distance x; now, the evolution will be defined by a time y, rather than a distance).
请注意,这并不意味着我们必须改变我们的方程,因为要使它们适合于这些更普遍的心理实验,就需要在实验设置中定义我们术语的值依赖于时间。不过,这在某种程度上已经做到了,这就是为什么gydF4y2Ba.全面地说,我们现在看到等式31更准确地描述为具有系统所描述的系统的概率gydF4y2Ba在一个状态下崩溃gydF4y2Ba.这将是:gydF4y2Ba
请记住,公式32适用,如果且仅当国家gydF4y2Ba而它们相应的进化可以被描述为它们之间的相互干扰,这种干扰通过某种方式(无论其性质如何)或贯穿时间而延长。gydF4y2Ba
Schrödinger的等式gydF4y2Ba
Schrödinger的方程建立了任何量子系统的演变gydF4y2Ba在时间t评估gydF4y2Ba
在哪里gydF4y2Ba是表示系统演变的矩阵。正如我们可以将所有系统定义为添加所有可能的状态,gydF4y2Ba
我等于系统可能的状态数,agydF4y2BangydF4y2Ba复数是-,我们可以展开方程33来得到gydF4y2Ba
考虑到这一点,我们可以创建一组方程,使我们能够同时评估有系统的概率,该概率地利用等式32和35使用等式的空间点和其哈密顿演进的概率。gydF4y2Ba
使用该组的实用性依赖于它允许用户以并行方式分析的概率,该概率在特定点处具有着陆的量子系统,并且如果达到这一点,它将是它的演化。gydF4y2Ba
此外,这两种分析量子演化的方法的核心区别在于实用上的便利。当有一个粒子要遵循的路径时(这意味着多重进化),选择我们的泛化可能会更方便。然而,当系统的基本状态在确定的时间跨度内不断演化时,应用Schrödinger的方程更为直接。gydF4y2Ba
结论与总结性总结gydF4y2Ba
从整体上讲,通过这个方程,有可能将运动中的量子系统的演化概括为一组确定的制定操作gydF4y2Ba
式中,y为诱导状态干扰装置的个数。gydF4y2Ba
只要评估的量子系统被限制在一个位移上,这个位移与一个可能的演化有关,这是由于波函数的推论,它描述了包含确定性质的可能状态[1-10]。gydF4y2Ba













